


Wind, Water & – Math?
by Kathleen Cason


When Ming-Jun Lai took
his family river rafting in the North Carolina mountains, they meandered
past stunning scenery, hurtled through rapids and then came to an abrupt stop.
“We were just too close to this rock,” said Lai, a University of Georgia mathematics professor.
The current grabbed the raft, swept it behind a big rock and briefly trapped raft and rafters in a
large eddy. “This was really exciting,” he said.
And quite predictable, if like Lai, you know how to do the math.
Lai and fellow UGA mathematician Paul Wenston specialize in applied mathematics. For years they
have been working on a classical mathematics problem — the Navier-Stokes equation — that describes
how fluids move. The pair developed an innovative way to approximate solutions to equations that
would have predicted, among other things, the raft’s path into the eddy.
In the 19th century, French engineer Claude Navier and Irish mathematician George Stokes
independently devised a system of partial differential equations that describe how fluids move when
subjected to forces. Today, Navier-Stokes equations might help engineers design faster boats,
optimize ink flow in ink jet printers or perfect the shape of airplane wings. Mathematicians also
might use these equations to track the ocean’s currents or render computer animations of water
in films like Finding Nemo or The Perfect Storm.
As yet, however, no one has been able to prove the uniqueness of the solution of Navier-Stokes
equations, considered one of the seven greatest unsolved mathematical puzzles both because of
difficulty and central importance to modern mathematics. The Clay Mathematics Institute in
Cambridge, Mass., even offers a $1 million prize to anyone who solves the puzzle.
Lai and Wenston are not millionaires yet, but they have invented a method that uses “multivariate
splines” to numerically approximate solutions to Navier-Stokes equations.
Splines are mathematical representations of smooth curves that can be used, for example, in font
design to ensure that letters have smooth edges no matter how big. Multivariate splines extend the
idea to three-dimensional surfaces. For instance, to mathematically describe the hood of a car, the
hood’s surface is divided into many triangles so that a simple formula representing the surface
over each triangle can be derived. The triangle formulas are pieced together like facets of a
diamond to describe the more complex surface of the hood. Then multivariate splines smooth the
edges where the triangles meet to better approximate the real object.
When applied to Navier-Stokes equations, the multivariate spline method reduces approximation
errors much better than the standard approach, called the finite element method.
Ardent followers of the finite element method around the world are beginning to accept the Lai and
Wenston method as a better way to numerically analyze Navier-Stokes equations, said Dan Kannan,
head of UGA’s mathematics department.
Lai and Wenston haven’t limited their application of multivariate splines to Navier-Stokes
equations. The two mathematicians have used the approach to tackle the math behind compressing
digital photographic images, simulating air flow over cars, modeling water flow through channels
and mixing fluids of different viscosities, which has implications for chemical spills.
Their latest project is a collaborative effort with Ohio State University scientists. Funded by a
National Science Foundation grant, the team will use multivariate splines to model the Earth’s
gravitational field. The availability of powerful computers is making it possible for the
researchers to develop a more accurate model of the gravitational field, one that takes into acount
the small changes that occur due to events like earthquakes, landslides or glaciers. A more precise
gravitational model in turn will enhance the accuracy of other models that include gravitation as a
variable, such as those that predict weather or chart ocean currents.
For more information, contact Ming-Jun Lai at mjl@math.uga.edu or Paul Wenston at
paul@math.uga.edu.
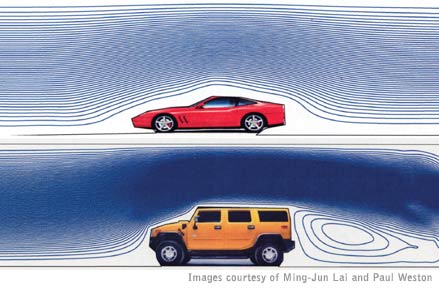 Predicting how air flows over a car is among the applications of research by UGA mathematicians Ming-Jun Lai and Paul Wenston. The Ferrari's sleek design (top) reduces drag and increased fuel efficiency compared with a Hummer H2.
Predicting how air flows over a car is among the applications of research by UGA mathematicians Ming-Jun Lai and Paul Wenston. The Ferrari's sleek design (top) reduces drag and increased fuel efficiency compared with a Hummer H2.
For comments or for information please e-mail the editor: jbp@ovpr.uga.edu
To contact the webmaster please email: ovprweb@uga.edu
![]()